
लेखाची सुरुवात अशा एखाद्या भारदस्त वाक्याने करावयास मिळावी, अशी माझी फार इच्छा होती. परंतु माझ्या दुर्दैवाने हा संदर्भ अजिबात खरा नाही. हा खरा तर लेखाची तयारी करताना माझ्याच मनात आलेला विचार आहे. प्रेमात पडल्यावर जगण्याकडे बघायचा 'नजरिया' बदलून जातो, काहीतरी वेगळे जाणवायला लागते, लाल टायसुद्धा आवडायला लागतो इत्यादी परिणाम सुज्ञांना ज्ञात असतीलच. पॅराडाइम शिफ्ट म्हणजे असाच दृष्टिकोनातील बदल म्हणता येईल; कुठल्यातरी प्रचलित गृहीतकाला धक्का देऊन होणारा, ज्याने प्रचंड उलथापालथ होऊ शकते असा बदल. म्हणूनच यास 'क्रांतिकारी बदल' म्हटले जाते. टॉलमी आणि कोपर्निकस या दोघांनीही आपापल्या परीने ग्रहांच्या कक्षा रेखाटण्याचा प्रयत्न केला. परंतु टॉलमीने त्या काळात प्रचलित असलेल्या 'ग्रहांच्या कक्षा वर्तुळाकारच असल्या पाहिजेत' या विचाराच्या चौकटीत राहून त्या रेखाटल्या, तर कोपर्निकसने 'त्या लंबवर्तुळाकार (एलिप्टिकल) आहेत' हा आधीच्या विचाराला छेद देणारा नवीन विचार मांडला. एकाच प्रश्नाची ही दोन्ही शक्य उत्तरे होती, परंतु कोपर्निकस अर्थातच बरोबर ठरला आणि त्याच्या विचारांतून भौतिकशास्त्रातली पुढची प्रगती शक्य झाली. विविध विचारधारांमध्ये शतकानुशतके असे बदल होत आले आहेत. गणितामधल्या काही क्रांतिकारी बदलांचा संक्षिप्त परामर्श घेण्याचा हा प्रयत्न.
स्थानिक किमतीची पद्धत आणि शून्याचा शोध:
आदिमानव दगडांवर रेषा आखून गुरे मोजत होता, ही गोष्ट सर्वांना माहीत असेल. जवळपास ५०,००० वर्षांपूर्वी मोजण्याची क्रिया मानवाला करता येत होती, असे पुरावे उपलब्ध आहेत. संख्या मोजण्याबरोबर त्या लिहायच्या कशा, हाही प्रश्न आला. 'बॅबिलोनिअन न्यूमरल्स्' ही संख्या लिहिण्याची जगातली पहिली पद्धत मानली जाते. सुमेरिअन संस्कृतीत ही पद्धत शोधली गेली व तेथून ती बॅबिलोनिअन संस्कृतीकडे गेली, असा काहींचा दावा आहे. ख्रि.पू. ३०००च्या सुमारास प्रचलित झालेली ही पद्धत स्थानिक किमतीवर आधारित होती. याचाच अर्थ, कुठला अंक संख्येमध्ये कुठल्या स्थानावर आहे, यावर त्या अंकाची किंमत ठरत असे. आजची दशमान पद्धत यावरच आधारलेली आहे. उदाहरणार्थ, १२ या संख्येमध्ये १ या आकड्याची किंमत १० आहे, तर २१ या संख्येमध्ये १ या आकड्याची किंमत १ एवढी आहे. दशमान पद्धत आपल्या १० या संख्येवर आधारित आहे, तर बॅबिलोनिअन पद्धत आपल्या ६० या संख्येवर आधारित होती. जगातील पहिली संख्यालेखनाची पद्धत, आणि स्थानिक किमतीचा वापर या आधारावर हा एक क्रांतिकारी बदल आहे, असे म्हणायला हरकत नाही.

बॅबिलोनिअन पद्धतीतील चिन्हे
बॅबिलोनिअन पद्धतीत 'शून्य' दर्शविण्यासाठी रिकामी जागा सोडत. मात्र त्यांच्या पद्धतीत संख्या कोठे संपते, याची कल्पना येणे शक्य नसल्याने संख्येतील सर्वांत उजवीकडील अंकाच्या उजवीकडे 'शून्य' आहे की नाही, हे अंदाजानेच समजत असे. उदाहरणार्थ, २ ही संख्या बॅबिलोनिअन पद्धतीत २ किंवा २० = २ गुणिले ६० किंवा २०० = २ गुणिले ६० गुणिले ६० अशीही वाचता येईल. बॅबिलोनिअन लोकांना शून्याचे महत्त्व थोडेफार प्लेसहोल्डर म्हणून कळले होते, परंतु त्यांनी एक चिन्ह (सिम्बल) म्हणून किंवा एक संकल्पना म्हणून त्याचा विचार केला नाही, असे दिसते.
याचबरोबर 'रोमन न्यूमरल्स्' ही पद्धतदेखील रोमन साम्राज्यामध्ये विकसित झाली होती. या पद्धतीत लिपीतील अक्षरांचा वापर विशिष्ट आकडे म्हणून केला जाई. I म्हणजे १, V म्हणजे ५, X म्हणजे १०, C म्हणजे १०० ही चिन्हे सर्वांनीच कधी ना कधी पाहिली असतील. यात स्थानिक किमतीचा अवलंब केला जात नसे. या संख्यांची बेरीज संख्या एकमेकांना जुळवून केली जाई. उदाहरणार्थ, II म्हणजे १ + १ = २ होय. या संख्या लिहिणे व त्यांच्या बेरजा-वजाबाक्या करणे हे बरेच क्लिष्ट काम होते.
याशिवायही काही पद्धती अस्तित्वात होत्या. ग्रीक पद्धत, ज्यावरून पुढे रोमन पद्धत उदयास आली, ही दशमान पद्धत आणि (नंतर आलेली) रोमन पद्धत यांचा संकर होती. परंतु यात स्थानिक किमतीची पद्धत वापरली नव्हती. यातदेखील अंक दर्शविण्यासाठी अक्षरांचा वापर केला जाई. दिग्गज ग्रीक गणितज्ञांनी ही पद्धत वापरली, परंतु त्यांच्या लिखाणात शून्याचा उल्लेख किंवा कमीतकमी प्लेसहोल्डर म्हणून वापर दिसून येत नाही. (निदान माझ्या वाचण्याततरी नाही.)
या सर्वांत क्रांतिकारी बदल घडवून आणला, तो भारतीय गणितज्ञांनी. भारतीय गणितज्ञांनी शून्याचे महत्त्व एक संकल्पना म्हणून जाणले, व त्यास ० हे चिन्ह दिले. ब्रह्मगुप्त हा शून्याचे संख्या म्हणून गुणधर्म सांगणारा पहिला गणिती होय. अ + ० = अ, अ - ० = अ, अ गुणिले ० = ०, ० - अ = - अ इत्यादी सर्व नियम ब्रह्मगुप्ताने इ.स. ६३८मधील 'ब्रह्मस्फुटसिद्धांत' या ग्रंथात प्रथम सांगितले [१]. आर्यभट्टाचे कामही यासंदर्भात महत्त्वाचे आहे. आर्यभट्टाने इ.स. ४९८च्या सुमारास 'स्थानात् स्थानम् दशगुणम् स्यात्' अर्थात 'एका स्थानावरून दुसर्या स्थानी गेल्यावर किंमत दहापट होते,' असे लिहून ठेवले आहे. ब्रह्मगुप्त आणि आर्यभट्टाच्या कामातून हिंदू-अरेबिक पद्धतीचे पहिले पाऊल पडले. त्यावर अरेबियन गणितज्ञांनी साज चढवून ही पद्धत युरोपात नेली आणि आजपर्यंत तीच प्रचलित आहे. गुणाकाराचे, भागाकाराचे नियम या पद्धतीमुळे सोपे होतात. ब्रह्मगुप्ताने स्वतः अपूर्णांकांच्या बेरजा-वजाबाक्यांचे नियम त्याच्या ग्रंथात दिलेले आहेत.
शून्य या संख्येच्या उगमामुळे द्विमान (बायनरी) पद्धतीसारख्या १०ऐवजी कुठल्याही संख्येवर अवलंबून असणार्या पद्धती सुटसुटीतपणे विकसित करता येतात. (खरेतर पिंगल या भारतीय गणितज्ञाने इसवी सनाच्या पूर्वीच द्विमान पद्धत वापरली होती, असे दिसते.) द्विमान पद्धतीतून विसाव्या शतकात आधुनिक संगणकशास्त्राचा पाया घातला गेला. या क्रांतिकारी कल्पनांचे परिणाम दूरगामी आणि बहुआयामी आहेत.
अशा रीतीने स्थानिक किमतीची कल्पना, शून्याचा शोध आणि दशमान पद्धतीचा उगम हे गणितातील पॅराडाइम शिफ्ट आहेत, असे म्हणता येते. (खरे तर नवीन पॅराडाइमची सुरवात.) आधुनिक गणिताचा पाया घालण्यात यांची मोठी मदत झाली.
भूमिती: यूक्लीडीय ते अयुक्लिडीय
अंकांच्या जगात या घडामोडी चालू असताना गणितातल्या बाकीच्या शाखा मागे राहणे शक्यच नव्हते. ख्रि.पू. ३००च्या आसपास अलेक्झांड्रिया गावी यूक्लीड हा ग्रीक गणितज्ञ कार्यरत होता. यूक्लीडने नंबर थिअरी व भूमिती या शाखांमध्ये महत्त्वाची कामगिरी बजावली. विशेषतः भूमितीमध्ये यूक्लीडचा 'एलेमेंट्स्' हा ग्रंथ अगदी विसाव्या शतकापर्यंत प्रमाणभूत मानला जाई. या ग्रंथाची झेप त्याआधीच्या पुस्तकांच्या इतकी पुढे होती, की ती पुस्तके कुणीही जतन न केल्याने काळाच्या ओघात जवळपास सर्वच गडप झाली. 'एलेमेंट्स्'मधील काही सिद्धांत त्याआधीही गणितज्ञांना परिचित होते, परंतु यूक्लीडचे मोठे यश हे, की त्याने एकाच तर्कसंगत चौकटीत सर्व काम बसवले. त्यामुळे वापरास आणि संदर्भास ते अतिशय सोपे झाले. रिगरस प्रूफ अर्थात काटेकोर सिद्धतेची पद्धत गणितामध्ये रूढ करण्यामध्ये त्याचा मोठा हातभार लागला. अॅक्झिओमॅटिक फ्रेमवर्क (Axiomatic Framework), म्हणजेच काही गृहीतके सुरुवातीस घेऊन त्यांपासून वेगवेगळे निष्कर्ष काढणे, याची सुरुवात यूक्लीडपासून झाली, असे म्हणावयास हरकत नाही. भूमितीची सुरुवात करून यूक्लीडने पॅराडाइम शिफ्ट घडवून आणली. ज्या गृहीतकांवर यूक्लीडची भूमिती आधारित आहे ती प्रसिद्ध आहेत -
(१) कुठल्याही दोन बिंदूंमधून जाणारा सरळ रेषाखंड काढता येऊ शकतो.
(२) कुठलाही रेषाखंड अनंतापर्यंत वाढवून त्याचे रेषेत रूपांतर करता येते.
(३) कुठलाही रेषाखंड दिला असता त्याचा एक अंत्यबिंदू हा केंद्रबिंदू असलेले आणि त्याच्या दुसर्या अंत्यबिंदूमधून जाणारे वर्तुळ काढता येते.
(४) सर्व काटकोन एकरूप आहेत.
(५) जर एक रेषाखंड दिलेल्या दोन रेषांना अशा प्रकारे छेदत असेल, जेणेकरून त्यांच्यातील आंतरकोनांची बेरीज दोन काटकोनांपेक्षा कमी होत असेल, तर त्या दोन रेषा अनंतापर्यंत वाढवल्यास ज्या बाजूस आंतरकोनांची बेरीज दोन काटकोनांपेक्षा कमी होत आहे, त्या बाजूस एकमेकांना छेदतील. (समांतर रेषांचे गृहीतक)
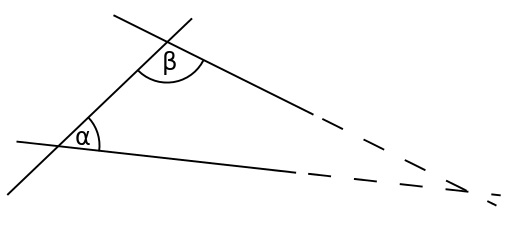
समांतर गृहीतक
या गृहीतकांशिवाय अनेक व्याख्या यूक्लीड देतो. या व्याख्यांच्या व गृहीतकांच्या साहाय्याने मग यूक्लीड अनेक विधानांची सिद्धता देतो. यूक्लीडची ही गृहीतके अत्यंत किमान स्वरूपाची आहेत. उदाहरणार्थ, 'दिलेल्या रेषाखंडाएवढ्या लांबीचा रेषाखंड दुसर्या रेषेवर काढणे' ही क्रिया करताना आपण कर्कटकाचे एक टोक रेषाखंडाच्या एका अंत्यबिंदूवर ठेऊन दुसरे टोक दुसर्या अंत्यबिंदूवर ठेवून तो उचलून दुसर्या रेषेवर ठेवून तेवढेच अंतर मिळवतो. परंतु यूक्लीडच्या जगात या क्रियेला स्थान नाही, कारण त्याचा कर्कटक हवेत उचलला, की तो मिटतो! असे असले, तरीसुद्धा फक्त वरील गृहीतकांपासून ही क्रिया करणे शक्य आहे! वाचकांनी स्वतः प्रयत्न करून पाहावा! खरेतर ही इतकी साधी गोष्ट आहे की, यूक्लीडने हिचादेखील समावेश या गृहीतकांत केला असता, तरी काही विशेष नाही. परंतु यूक्लीडने केवळ ज्यांची सिद्धता करता येत नाही अशाच गोष्टी गृहीतके म्हणून घेण्याचा काटेकोरपणा पाळला. याबाबतीत त्याची नाडी गणिताच्या मूळ तत्त्वाशी जुळली, असे म्हणावयास हरकत नाही.
सौंदर्याधिष्ठित सत्यशोधन हे गणिताचे मूळतत्व किंवा गाभा आहे असे म्हणता येईल. ह्यातील सत्यशोधनास अर्थात सर्वाधिक महत्त्व आहे. एखादी चुकीची सिद्धता केवळ ती सुंदर दिसते म्हणून स्वीकारता येणार नाही. मात्र बरोबर असलेली सिद्धता कितीही क्लिष्ट, कृत्रिम आणि विद्रूप वाटत असली, तरीही ती स्वीकारार्ह असते. परंतु गणितज्ञाचे मन फक्त प्रश्नांच्या सिद्धता शोधून थांबत नाही, तर त्यांनी गणिताच्या जगड्व्याळ चित्रात सुंदर रंग भरावे, असेही त्याला वाटत असते. नवनवीन संकल्पना शोधून काढून एखादी बरोबर, पण क्लिष्ट सिद्धता या संकल्पनांच्या चौकटीत बसवून कशी सोपी करता येईल, ह्यासाठीही गणितज्ञांचा प्रयत्न चालू असतो. ह्याच प्रयत्नातून पुढे नवीन मार्ग मोकळे होणार असतात. अशा प्रकारचा प्रयत्न सर्वप्रथम करणार्यांमध्ये यूक्लीड हा एक अग्रगण्य गणिती. त्यामुळेच त्याचे ऋण मोठे आहे.
यूक्लीडने वरील पाच विधाने गृहीतक म्हणून धरली. यांतील पहिली चार विधाने इतकी साधी आणि मूलभूत आहेत की, त्यांची सिद्धता देता येणे अशक्यच वाटते. (किंबहुना त्या स्वयंसिद्ध वाटतात.) परंतु पाचव्या विधानात जरा गडबड वाटते. ते स्वयंसिद्ध वाटत नाही. यूक्लीडने हे विधान पहिल्या चार विधानांच्या साहाय्याने सिद्ध करायचा बराच प्रयत्न करून शेवटी नाईलाजाने ते पाचवे गृहीतक म्हणून घेतले, असे मानायला जागा आहे. अनंतापर्यंत रेषा वाढवत नेल्यावर त्या छेदतील की नाही ते कसे ठरवायचे, असा काहीसा या गृहीतकाला असलेला आक्षेप आहे. पुढे आपण या गृहीतकाचे अजून एक रूप बघू, ज्यात हा आक्षेप अजून स्पष्ट होईल.
यूक्लीडनंतरच्या बर्याच गणितज्ञांनी शतकानुशतके समांतर रेषांच्या या गृहीतकाची सिद्धता देण्याचा प्रयत्न केला. यात टॉलमी, ओमर खय्याम अशांचा समावेश होता. रुबायांसाठी प्रसिद्ध असलेला ओमर खय्याम तो हाच. त्याचे गणितातदेखील महत्त्वाचे काम आहे! आधुनिक काळाच्या आधी बीजगणितावर लिहिल्या गेलेल्या महत्त्वाच्या ग्रंथांमध्ये त्याच्या एका ग्रंथाचा समावेश होतो. टॉलमीची सिद्धता चुकीची होती, तर ओमर खय्यामने त्याच्या प्रयत्नात काळाच्या थोडी पुढे उडी मारून अयूक्लीडीय भूमितीतील काही प्रमेये शोधून काढली, परंतु त्याला त्यांचा फारसा अंदाज लागला नाही.
या सर्व चुकलेल्या प्रयत्नांतून समांतर रेषेच्या गृहीतकाची अनेक रूपे समोर येत गेली (reformulations), वेगवेगळ्या प्रकारे हे गृहीतक मांडण्याचे प्रयत्न केले गेले. त्यातील सर्वांत महत्त्वाचे ठरलेले रूप पुढीलप्रमाणे -
एक रेषा आणि तीवर नसलेला कोणताही बिंदू दिला असता, त्या बिंदूमधून जाणारी व दिलेल्या रेषेला समांतर अशी एक आणि एकच रेषा काढता येऊ शकते.
टीप - लक्षात ठेवण्यासारखी गोष्ट म्हणजे खरे तर निव्वळ हे विधान आणि समांतर रेषेचे गृहीतक एकमेकांना समानार्थी नाहीत. परंतु पहिल्या चार गृहीतकांच्या उपस्थितीत ती एकमेकांना समानार्थी आहेत.
या विधानाला घेता येणारा आक्षेप असा (जो आधीच्या गृहीतकाच्या आक्षेपाशी निगडित आहे), की अनंत अंतरावर काय होते आहे, ते माहीत नसल्याने कदाचित एकही समांतर रेषा काढता येणार नाही, किंवा एकापेक्षा अधिक समांतर रेषा काढता येतील. या आक्षेपावर विश्वास बसणे थोडे अवघड आहे, परंतु पृथ्वीच्या पृष्ठभागाचे उदाहरण घेऊन बघा. दोन रेखांश हे विषुववृत्ताजवळ एकमेकांना समांतर असतात / वाटतात, परंतु शेवटी ते उत्तर आणि दक्षिण धृवांशी एकमेकांना छेदतात. तुम्ही म्हणाल, रेखांश तर वर्तुळाकार आहेत व आपले विधान रेषांशी संबंधित आहे. परंतु पृथ्वीच्या वक्र पृष्ठभागावर सरळ रेषा अशी काढता येणारच नाही, हीच त्यातली गंमत आहे. यूक्लीडची भूमिती ही प्रतलीय भूमिती आहे. मात्र वक्र पृष्ठभागांवर सरळ रेषा म्हणजे काय? या प्रश्नाचे उत्तर देण्यासाठी बरेच डोके खाजवावे लागते. वक्रपृष्ठीय रेषेची (जीओडेसिक, Geodesic) कल्पना यातून पुढे आली. पुढील चित्रातून ही गोष्ट जास्त स्पष्ट होईल -
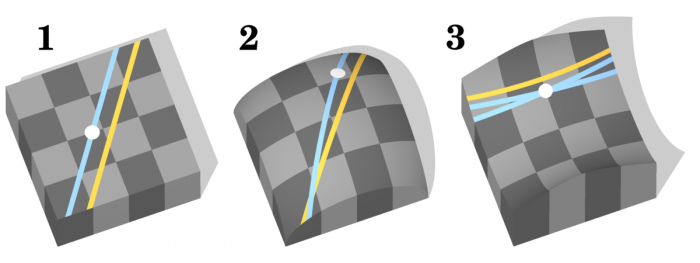
वरील आक्षेप हा मामुली तर्कदोष नसून तो आपल्या ज्ञानामधील उणीव दर्शवतो व या आक्षेपाचे खंडन करण्याचा प्रयास थांबवून त्यास सामावून घेता येईल का, हे बघितले पाहिज,, ही जाणीव १८व्या व १९व्या शतकामध्ये गणितज्ञांना व्हायला लागली. गणिताचा राजकुमार कार्ल फ्रेडरिख गॉस, याने १९व्या शतकाच्या सुरुवातीस या प्रश्नावर विचार केला, परंतु त्याने आपले काम कधीच प्रसिद्ध केले नाही. त्याच्यानंतर काही वर्षांत बोल्याई, लोबॅच्युवस्की, रिमान, पॉईंकारे या गणितज्ञांनी 'एलिप्टिकल जॉमेट्री' आणि 'हायपरबोलिक जॉमेट्री' या दोन, यूक्लीडची पहिली चार गृहीतके पाळणार्या, परंतु पाचवे गृहीतक न पाळणार्या भूमित्या शोधून काढल्या. या अयूक्लीडीय भूमित्या आहेत. वरील चित्रातील दुसरे चित्र हे एलिप्टिकल जॉमेट्री दर्शवते, तर तिसरे चित्र हायपरबोलिक जॉमेट्री दर्शवते. यामधून यूक्लीडची भूमिती चूक ठरत नाही. फक्त ती सर्वच ठिकाणी वापरता येत नाही, हे दिसून येते, म्हणजेच तिच्या मर्यादा स्पष्ट होतात. अशा रीतीने या गणितज्ञांनी भूमितीमध्ये पॅराडाइम शिफ्ट घडवून आणली. ख्रि.पू. ३०० सालातल्या यूक्लीडने घडवून आणलेल्या पॅराडाइम शिफ्टच्या पायावर या गणितज्ञांनी पुढचा दगड बसवला, असे म्हणायला हरकत नाही. या प्रत्येक जॉमेट्रीवर एक वेगळा लेखच लिहिता येईल. याचबरोबर १८६८मध्ये बेल्ट्रामी या गणितज्ञाने यूक्लीडच्या पहिल्या चार गृहीतकांपासून पाचवे गृहीतक सिद्ध करता येत नाही, हे दाखवून दिले आणि शतकानुशतके चाललेले प्रयत्न अखेरीस थंड पडले.
गणितीय विश्लेषण (Mathematical Analysis) आणि काटेकोरपणा
भूमितीमध्ये पाचव्या गृहीतकाच्या सिद्धतेचा शोध शतकानुशतके चालू होता. दरम्यान युरोपात प्रबोधनाचे वारे वाहू लागले होते. विज्ञानात नवनवीन शोध लागत होते. भौतिकशास्त्राची प्रगती चालू होती. बीजगणित आणि भूमिती याना जोडणारा 'अॅनालिटिकल जॉमेट्री' अर्थात आपण शाळा-कॉलेजमध्ये शिकतो ती सहनिर्देशांकाच्या (कोओर्डिनेटस) साहाय्याने भूमिती रेने देकार्तने शोधून काढली होती. भूमितीमधील आकृत्या या बीजगणितीय समीकरणांनी मांडता येतात, हा विचारसुद्धा एक पॅराडाइम शिफ्ट आहे.
याच काळात गणितज्ञांना विविध बदलांचा अभ्यास करणारी गणिताची शाखा (Mathematics of Change) निर्माण करायची गरज भासू लागली होती. (गणितामधील बदलांवरील लेखात 'बदलाचे गणित' यावर न लिहून कसे चालेल? असा लेख लिहिल्याबद्दल गणितानेच आमचा बदला घेतला नाही, म्हणजे मिळवली). निरंतर (Continuous, non-ending नव्हे) बदल कसे होतात, त्यांची गती कशी मिळवावी, असे प्रश्न पुरातन ग्रीक गणितज्ञांपासून सर्वांना सतावत होते. त्यातून 'झेनोच्या विरोधाभासांचा' उदय झाला होता. शेवटी सतराव्या शतकात न्यूटन आणि लायब्निझ यांसारख्या दिग्गज गणितज्ञांनी कलनशास्त्राची (कॅल्क्यूलस) निर्मिती करून या प्रश्नांची समाधानकारक उत्तरे दिली. सूक्ष्म राशीचा (Infinitesimal Quantities) अभ्यास करून न्यूटन आणि लायब्निझ यांनी हे प्रश्न सोडवले. या प्रक्रियेत त्यांनी फलाच्या (function) मर्यादाबिंदूंचा (लिमिट्स्,limits) वापर केला. (ही फंक्शन्स् कशी बदलतात, याचा अभ्यास म्हणजेच बदलाचे गणित होय.)
लिमिटची संकल्पना ही गणितातील महत्त्वाची संकल्पना आहे. एखाद्या फलाची (function) एका विशिष्ट बिंदूभोवती वर्तणूक अभ्यासण्यासाठी तिचा उपयोग होतो. थोडक्यात सांगायचे झाले, तर बिंदूंचा एखादा क्रम (सिक्वेन्स) तुमच्या विशिष्ट बिंदूकडे कन्वर्ज होत असेल, तर त्या सिक्वेन्सवर तुमच्या फलाच्या किमती कुठे कन्वर्ज होतात, त्याचा अभ्यास करणे म्हणजे त्या फलाचे त्या बिंदूभोवती लिमिट काढणे होय. जर फलाचा आलेख (ग्राफ) तुमच्या समोर असेल, तर क्ष-अक्षावर तुम्ही फलाचा इनपुट थोडासा बदललात, तर य-अक्षावर फलाचा आउटपुट कसा बदलतो, याचा हा अभ्यास आहे.
अंतःप्रेरणेने (इंट्यूशनली) ही व्याख्या थोडा विचार केल्यास अगदी सहज वाटू शकते, परंतु ही काटेकोर व्याख्या नाही. कन्वर्जन्स ही संकल्पना या व्याख्येत आहे, जिची व्याख्या आधी कुठेही झालेली नाही. अंतःप्रेरणेने ही संकल्पना कळल्यासारखी वाटते, परंतु ती तितकीशी सोपी नाही. त्या काळातील मोठ्या गणितज्ञांकडून या बाबतीत साध्यासाध्या चुका घडलेल्या आहेत. कलनशास्त्रामध्ये अनंत संख्यांच्या बेरजा करणे हादेखील कन्व्हर्जन्स या संकल्पनेचा भाग आहे. लिओनार्ड ऑयलरने त्यांचा अभ्यास करताना
१ - १ + १ - १ + १ - १ + ... = १/२
आणि
१ - २ + ३ - ४ + ५ - ६ + ... = १/४
असे निष्कर्ष लिहून ठेवले आहेत. ही दिसायला विचित्र आणि चुकीची वाटणारी विधाने कन्व्हर्जन्सची काटेकोर व्याख्या न केल्याचा परिणाम होत.
या सर्वांचे मूळ कारण म्हणजे अनंताचा अभ्यास करताना आपली अंतःप्रेरणा कामी येत नाही. या काळापर्यंत बीजगणितात आणि भूमितीमध्ये अनंत गोष्टींची कल्पना कुणी केली नव्हती. परंतु आता मात्र याची गरज भासू लागली होती. त्यासाठी योग्य व्याख्या देणे आवश्यक होते. वरच्यासारख्या अनंत बेरजांचा नक्की अर्थ काय, हे समजणे आवश्यक होते. याची सुरुवात केली, ती बर्नार्ड बोल्झानो या बेल्जियन गणितज्ञाने. एकोणिसाव्या शतकाच्या पूर्वार्धात त्याने मॅथमॅटिकल अनॅलिसिस, अर्थात गणितीय विश्लेषण या शाखेची मुहूर्तमेढ रोवली. त्याने लायब्निझची सूक्ष्मराशी वापरून दिलेली लिमिटची व्याख्या झुगारून दिली व आधुनिक 'एप्सिलॉन-डेल्टा' व्याख्या दिली, जी आजच्या गणितात वापरली जाते. एका अर्थी आधुनिक गणिताचा व भौतिकशास्त्राचा पाया त्याने घातला. विश्लेषणामध्ये त्याने बरेच महत्त्वाचे सिद्धांत शोधले. दुर्दैवाने त्याची पुस्तके जवळपास पन्नास वर्षे विस्मृतीत पडून होती, व त्याचा यथोचित गौरव त्याच्या मरणानंतरच झाला. लिमिटची त्याची व्याख्यासुद्धा बर्याच गणितज्ञांना ज्ञात नव्हती.
ऑगस्टिन कॉशी हा या मालिकेतला दुसरा गणितज्ञ. याने बोल्झानोची व्याख्या स्वतः स्वतंत्रपणे शोधून काढली आणि त्यावर आधारित सिद्धता दिल्या. जुन्या सिद्धांतांच्या काटेकोर नसलेल्या सिद्धता त्याने सुधारून दिल्या. तसेच याने 'कॉम्प्लेक्स अॅनालिसिस' अर्थात काल्पनिक संख्यांचे विश्लेषण ही शाखा जवळजवळ एकहाती निर्माण केली. आज ही गणितात आणि भौतिकशास्त्रात जवळजवळ सगळीकडे वापरली जाते. त्यातील अनेक मूलभूत सिद्धांत कॉशीच्या नावावर आहेत. कॉशीचा त्याच्या काळातल्या आणि नंतरच्या गणितज्ञांवर मोठा प्रभाव आहे. जी. एच. हार्डी सारख्या गणितज्ञांनी त्याचे ऋण मान्य केलेले आहे.
कॉशीसारख्या गणितज्ञांकडूनदेखील कन्व्हर्जन्स समजण्यात काही चुका झाल्या होत्या. (म्हणजे बघा!) शेवटी कार्ल वेअर्स्ट्रास या गणितज्ञाने त्या उणिवा भरून काढल्या. त्याने 'यूनिफॉर्म कन्व्हर्जन्स'ची व्याख्या दिली आणि ती वापरून अनेक महत्त्वाचे सिद्धांत शोधले. तसेच बोल्झानोच्या पुस्तकांना त्याने वर आणले व त्याला योग्य तो मान मिळवून दिला. बोल्झानोच्या अनेक सिद्धांतांना त्याने अत्यंत व्यापक रूप दिले. त्याला आधुनिक विश्लेषणाचा जनक मानले जाते.
अशा रीतीने एकोणिसाव्या शतकात या गणितज्ञांनी गणिताकडे बघायच्या दृष्टीत व्यापक बदल घडवून आणला, अनेक नव्या शाखांना जन्म दिला आणि आधुनिक काळातील गणिताचा प्रारंभ केला.
उपोद्घात
क्रांतिकारी या शब्दात साधारणपणे 'पटकन होणारा' हा अर्थही अंतर्भूत असतो. त्याची व्याख्या संदर्भानुसार सोयीस्कररीत्या केली जाते. कुणा माणसाच्या आयुष्यात होणारा बदल एका रात्रीत होत असेल, एखाद्या व्यवसायात काही वर्षांच्या कालावधीत कायापालट होत असेल... आपण पाहिलेले सारे बदल मात्र जणू शतकानुशतके घडत आहेत. ज्या गणितज्ञांनी हे बदल प्रामुख्याने घडवून आणले, त्यांच्या धारिष्ट्याचे आणि कल्पनाशक्तीचे कौतुक करावे तितके थोडेच आहे, परंतु त्यांच्यामागे शतकानुशतकांची लपलेली तपश्चर्यादेखील होती, हे विसरून चालणार नाही. अस्तित्वातल्या प्रदेशातल्या सर्व वाटांचा मागोवा घेतल्याशिवाय नवीन प्रदेशाच्या सीमारेषा कुठे सुरू होतात ते सहसा कळत नाही. गणितातल्या सर्वच बदलांबद्दल हे खरे आहे आणि म्हणूनच न्यूटनला म्हणावेसे वाटले - If I have seen further it is by standing on ye sholders of Giants.
ज्या गणितज्ञांनी हे व असे बदल घडवून आणले, त्यांच्याबद्दल मी पामर काय बोलणार? त्यांच्यातील धैर्य, चिकाटी, हुशारी माझ्यात चिमूटभर जरी आली, तरी मी स्वतःला भाग्यवान समजेन. मानवजातीच्या 'सत्याच्या शोधाच्या प्रयत्नांत' ज्यांनी स्वतःला असे वाहून घेतले, त्यांची नावे इतिहासात अशी अजरामर झाली आहेत. गणिताशी त्यांचे नाते कायमचे जोडले गेले आहे. या लेखाद्वारे त्यांना आणि मानवजातीच्या ज्ञानाच्या पिपासेला एक कडकडीत सलाम!
तळटिप-
[१] - मात्र ब्रह्मगुप्ताची 'शून्याने भागाकार' या प्रश्नाच्या उत्तरात मात्र चूक झाली. हा खरोखर सखोल प्रश्न आहे आणि ब्रह्मगुप्तानंतरही अनेक गणितज्ञांनी या प्रश्नावर विचार केला. मात्र ०/० आणि अ/० म्हणजे किती? या दोन्ही प्रश्नांची उत्तरे समाधानकारकरीत्या मिळवायला अजून बरेच क्रांतिकारी बदल घडावे लागले. त्यास जवळपास १०००-१५०० वर्षे जावी लागली.
चित्रांचे तपशील-
चित्र क्र. १: © Josell7 (File:Babylonian_numerals.jpg) [GFDL (http://www.gnu.org/copyleft/fdl.html) or CC-BY-SA-3.0-2.5-2.0-1.0 (http://creativecommons.org/licenses/by-sa/3.0)], via Wikimedia Commons
चित्र क्र. २: © 6054 [GFDL (http://www.gnu.org/copyleft/fdl.html) or CC-BY-SA-3.0 (http://creativecommons.org/licenses/by-sa/3.0/)], via Wikimedia Commons
चित्र क्र. ३: "Euclidian and non euclidian geometry". Licensed under Creative Commons Attribution-Share Alike 3.0 via Wikimedia Commons - http://commons.wikimedia.org/wiki/File:Euclidian_and_non_euclidian_geome...
/File:Euclidian_and_non_euclidian_geometry.png





प्रतिसाद
अशा विषयांवर असे रंजक लेख
अशा विषयांवर असे रंजक लेख लहान वयात वाचायला मिळाले असते तर हे विषय आवडते झाले असते ! सुंदर लेख.
हा लेख आहे का ?का मला संपूर्ण
हा लेख आहे का ?का मला संपूर्ण लेख न दिसता टिपण दिसत आहे ?या २०१४ हितगुज दिवाळी अंकाचे तंत्र आमच्या मोबाईलशी कट्टी करते आहे वाटतं.
धन्यवाद दिनेश :)
धन्यवाद दिनेश :)
एकच नोंद करावीशी वाटते - 'कोपर्निकन क्रांती' मधून लंबवर्तुळाकार कक्षेचा विचार पुढे आला, हे खरे आहे, परंतु कोपर्निकसने तो स्वतः मांडला नव्हता. ब्राहे, केप्लर ह्या त्याच्या नंतरच्या पिढीतील खगोलशास्त्रज्ञांमुळे तो आला. कोपर्निकसने सूर्यकेंद्रित सूर्यमालेची कल्पना मांडली, जी ह्या बदलाची पहिली पायरी होती. लेख लिहिताना मी 'कोपर्निकन क्रांती'चा विचार करत होतो, त्यातून त्याबद्दल लिहीले गेले. ही तपशीलातील चूक माझ्या लक्षात बरीच नंतर आली, आणि मूळ लेखाला फार धक्का लागून संपादनाला उशीर होऊ नये, म्हणून मी ह्याची नोंद तेव्हा न करता आत्ता करत आहे. चुभूद्याघ्या.
भास्कराचार्य,
भास्कराचार्य,
ज्याची आतुरतेने वाट पाहत होतो त्या विषयावर लेख आला अखेरीस! :-) रंजक आणि रोचक लेख आहे. गणिताच्या रसिकांना असे लेख म्हणजे पर्वणीच. त्याबद्दल धन्यवाद.
क्रांतिकारी बदलांत डिराकचे डेल्टा फलन शोभून दिसले असते. तुमच्या मनात हा विचार नक्की आला असणार. मात्र विषय जरा जास्त किचकट असल्याने टाळला असावा, बरोबर?
आ.न.,
-गा.पै.
लेख छान झाला आहे.
लेख छान झाला आहे.
अजून मोठा असता आणि कनेक्टेड असता तर जास्त मजा आली असती. मधल्या जागा अजून लेख लिहून भरायला स्कोप आहे. डेसीमल प्लेसच्या अनुशंगानी इर्रॅशनल्स, फ्रॅक्टल वगैरे. हिलबर्टच्या प्रॉब्लेम्स बद्दलही.
लेख आवडला.
लेख आवडला.
गा. पै. , आतुरतेने लेखाची वाट
गा. पै. , आतुरतेने लेखाची वाट पाहिल्याबद्दल धन्यवाद. :) तांत्रिक गोष्टींबद्दल लिहिताना बरीच बंधने येतात, त्यामुळे डिराक डेल्टा सारख्या गोष्टी अशा लेखांत सध्या तरी न लिहायचे मी ठरवले होते. :) काही मूलभूत संकल्पनांची तोंडओळख वाचकांना झाली, तर त्यातच मला समाधान वाटेल.
aschig, येतील की अजून लेख! ;)
शोभनाताई आणि 'लेख आवडला' असे आवर्जून सांगणार्या सर्वांना धन्यवाद. :)
दिवाळीपूर्व उपक्रम
दिवाळीपूर्व उपक्रम
विविध जुन्या दिवाळी अंकांत प्रसिद्ध झालेले माबोकरांचे निवडक साहित्य